简介：
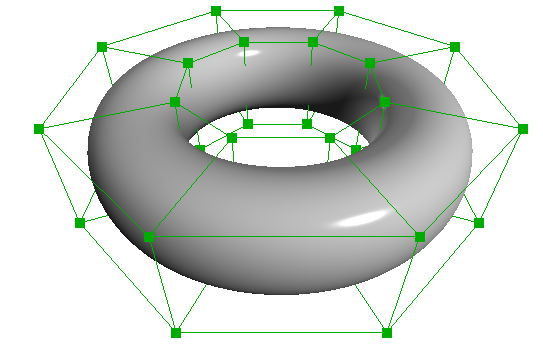
复杂模型要光滑表面的最常用的方法是：用 BSplines 或 NURBS 这样的双三次插值来模拟
然而，虽然它们确实提供了一个可靠的光滑极限曲面定义，
但双立方曲面仅限于二维拓扑结构，只能模拟真实世界中很小的一部分。
这种基本的参数限制，要求编写工具至少实现以下功能:
Smooth Trimming (平滑修剪)
Seams Stitching (拼接算法和接缝处处理)
裁剪和拼接都需要保证模型在空间和时间上的平滑。
要满足这些需求，则会增加复杂性和速度，
而细分曲面可以代表任意拓扑，因此不受这些约束。
任意拓扑结构
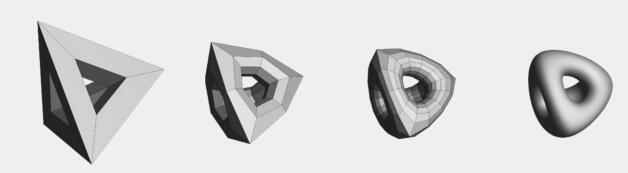
一个细分曲面，或参数曲面，可以说成是由点控制的网格，
它的原理是在网格表面，通过近似的插值，来控制网格的分段，从而达到光滑效果。
但是，如果多边形表面拥有足够多的数据点来控制平滑，那么一个平滑细分曲面：
无论表面的动画是怎样的，或者它被观察得多么清晰，多边形永远不会出现。
普通的立方 B 样条曲面都被转换为张量积(tensor-product)曲面的矩形网格。
也就是细分曲面将其转换为具有任意连通性的网格。
统一细分 Uniform Subdivision
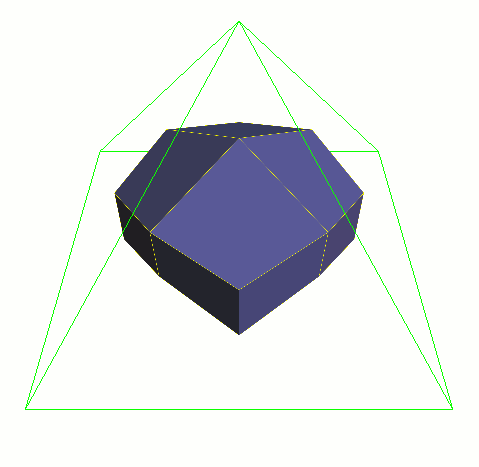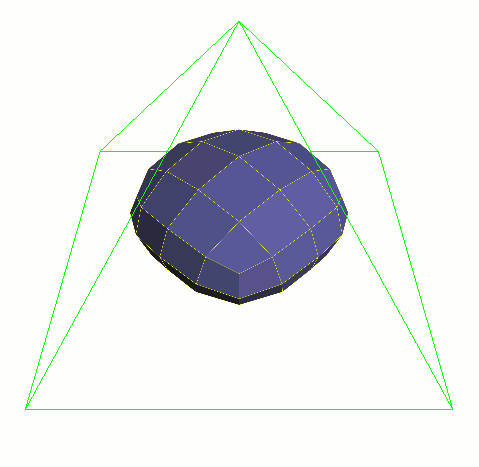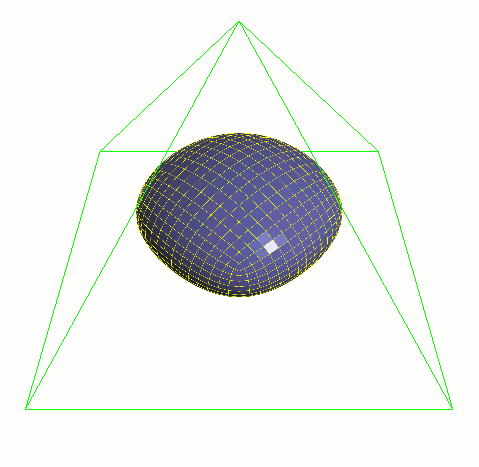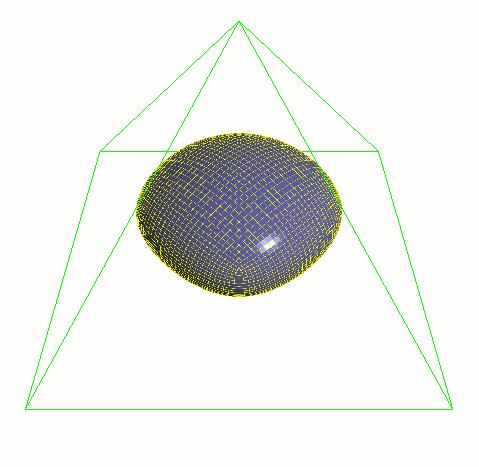
将统一细化方案应用于网格。算法的每一次迭代，网格都接近于细分曲面。
增加迭代次数时要格外谨慎。对每个迭代次数而言，对象中的顶点和多边形数（和计算时间）可以增加为原来的四倍。
对平均适度的复杂对象应用四次迭代会花费很长时间来进行计算。
自适应细分 Feature Adaptive Subdivision
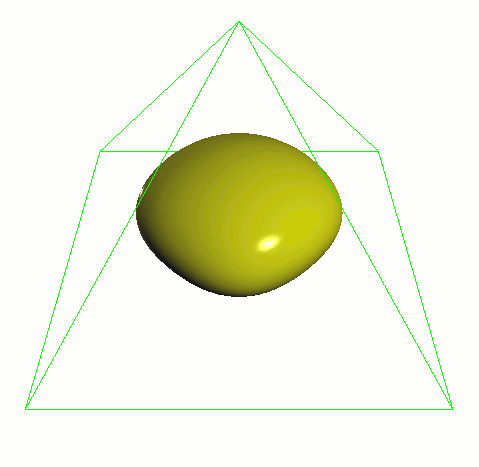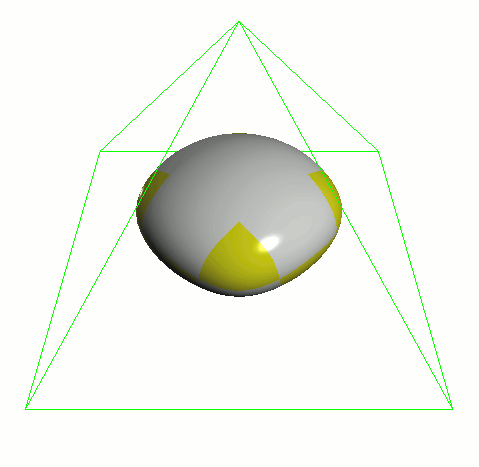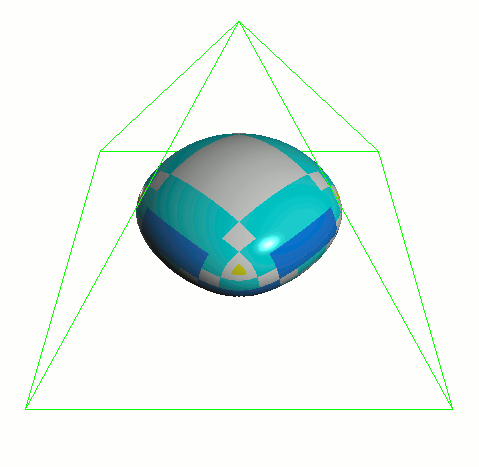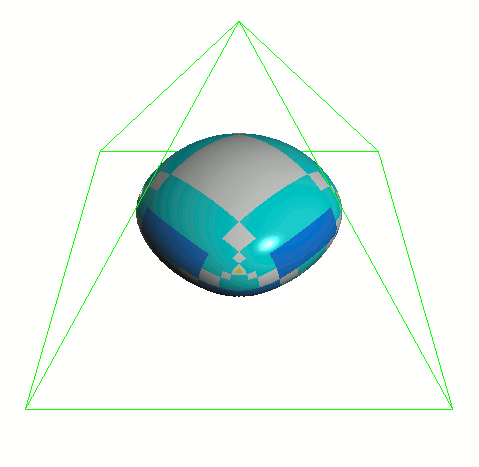
应用渐进的细分策略来隔离不规则的特性。由此产生的顶点可以组合成双立方算法来定义细分曲面。
统一还是自适应？
在时间和内存使用方面，特征自适应细化可以更为经济，但最好的使用方法取决于应用程序的需求。
下表列出了要考虑的几个因素：
统一的
指数几何增长
目前的实现只生成统一的细化的双线性补丁。
所有表面变化的插值规则支持在精炼的顶点位置。
特性自适应
几何生长接近线性，只出现在孤立的拓扑特征附近。
当前的实现只生成了用于特性自适应优化的双立方补丁。
目前，只有双线性的面变插值是支持双立方的。
边界插值规则 Boundary Interpolation Rules
边界插值规则控制边和顶点的插值。
下面的规则集可以应用于顶点数据插值:
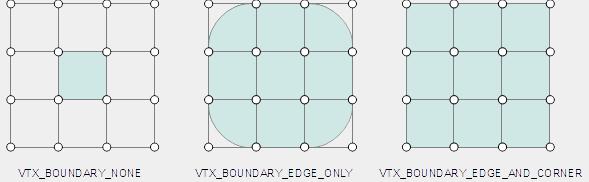
VTX_BOUNDARY_NONE: 无边界插值;相反，边界面被标记为孔，这样边界边链继续支持相邻的内部面，但不被认为是精细表面的一部分。
VTX_BOUNDARY_EDGE_ONLY: 所有边界边链都是尖锐的折痕;边界顶点不受影响。
VTX_BOUNDARY_EDGE_AND_CORNER: 所有的边界边链都是尖锐的折痕，而只有一个入射面的边界顶点是尖角。
面变化插值规则 Face-Varying Interpolation Rules
当表面上的数据不连续时，需要使用面变化的数据。通常是不相交的 UV 区域之间的接缝处。
表面变化的数据可以遵循与顶点数据相同的插值行为，也可以被限制为从各个角落、边界或整个网格内部的选择性特征上进行线性插值。
下面的规则可以应用于表面变化的数据插值，
这里的排序应用的是越来越多的线性约束：
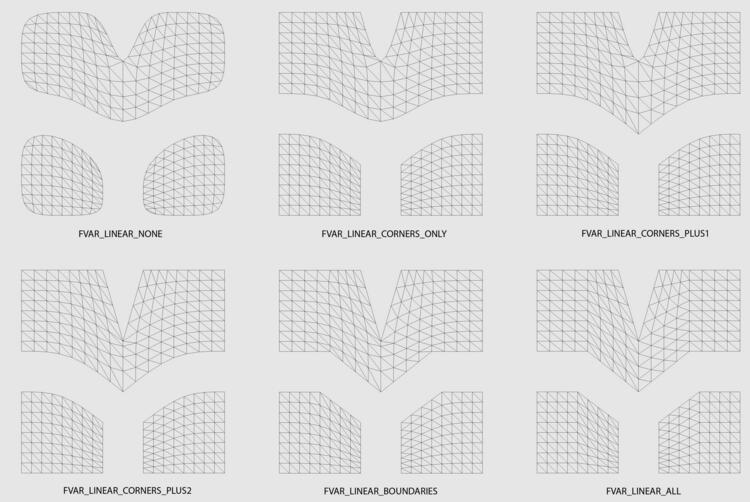
FVAR_LINEAR_NONE 平滑所有网格
FVAR_LINEAR_CORNERS_ONLY: 锐化（线性插值）拐角
FVAR_LINEAR_CORNERS_PLUS1: CORNERS_ONLY + 3 个或多个区域交界处的锐化
FVAR_LINEAR_CORNERS_PLUS2: CORNERS_PLUS1 + 尖锐的和凹角的锐化
FVAR_LINEAR_BOUNDARIES：沿所有边界和角的线性插值。
FVAR_LINEAR_ALL：内插值(边界和内部)
这些规则不能使 Face-Varying 数据的插值比顶点的平滑。
尖锐值、边界插值规则或细分方案本身（如双线性）所产生的网格的尖锐特征存在优先权。
利用 catmark_fvar_bound1 回归形状，在 UV 空间中显示的所有 Face-Varying 插值模式。
一个简单的 4x4 四分网格，分割为三个 UV 区域(它们的控制点位置隐含在 FVAR_LINEAR_ALL 中):
半清晰的折痕 Semi-Sharp Creases
它可以修改细分规则来创建分段光滑的表面，包括折痕和角等无限尖锐的特征。
作为一种特殊情况，曲面可以通过将边界标记为尖锐来插值它们的边界。
然而，我们已经认识到，现实世界表面从来没有真正的无限锋利的边缘，特别是当看得足够近。
为此，我们增加了半锐利折痕的概念，即可控锐度的圆形折痕。
这些允许您创建更类似于圆角和混合的特性。
当你标记边缘和边缘链为折痕时，它提供了从 0 到 10 的锐度值，锐度值>=10 被视为无限锐度。
应该注意的是，无限锐的折痕实际上是表面上的切线不连续，这意味着几何法线在那里也是不连续的。
因此，沿正常方向移动可能会沿折痕撕裂表面。
如果你真的想要在折痕上移动一个表面，那么最好是使折痕处于半锋利的状态。
Chaikin Rule 蔡金规则
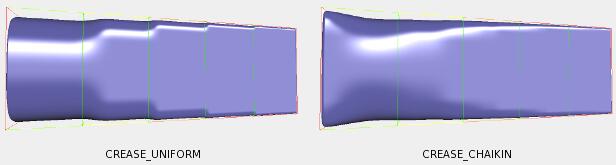
Chaikin 的曲线细分算法提高了具有不同权重的多边缘半锐折线的外观。Chaikin 规则插入了事件边缘的锐度。
连续半尖峰插值的例子:
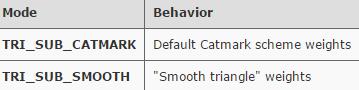
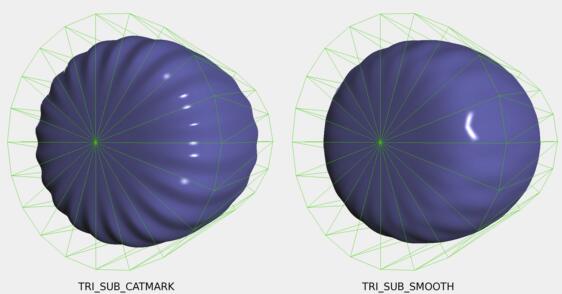
"Triangle Subdivision" Rule 三角形细分规则
三角剖分规则是加到 Catmull-Clark 方案中的一条规则，这个规则是凭经验确定使三角形细分更顺畅。
然而，这条规则打破了两个单独的网格可以通过重叠边界无缝连接的良好属性，即当两个边界上都有三角形时，不可能无缝地加入网格。
例子:
Manifold vs Non-Manifold Geometry 流形与非流形几何
连续极限曲面通常要求拓扑是一个二维流形，在有限曲面上是明确的。
对非流形几何建模是可能的（有时是有用的，有时只是暂时的），从而创建限制不明确的曲面，也就是曲面的界限没有被定义好。
下面的例子展示了非流形拓扑结构的典型例子：
Non-Manifold Fan
这个“fan”配置显示了一个由 3 个不同的面共享的边。
有了这种配置，目前还不清楚哪一个面应该贡献到极限面（假设它是单数），因为三个面具有相同的边。
fan 配置不限于三个面：任何配置两个以上的边共享的都会导致同样的问题。
这些和其他涉及非流形边缘的区域，是通过考虑“局部流形”的区域来处理的。
与许多面相比，在这个有问题的边缘上，没有一个单一的限制面，边缘局部将单一的限制面划分为多个。
因此，这三个面中的每一个都有它们自己的(局部流形)限制面——它们都在共享边界上相交。
Non-Manifold Disconnected Vertex
顶点与任何边和面断开连接。
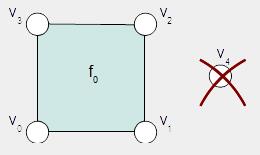
这个例子非常简单:对于四个顶点和它们定义的面有一个非常明确的限制面，
但是没有方法来精确地从断开的顶点确定一个限制面。
虽然顶点不影响任何极限表面，但它可能并不完全无关。
这样的顶点在细分时可能值得保留(如果没有其他原因，只是为了保留某些顶点的排序)，并且在考虑到极限表面的时候简单地忽略了。
原文地址 ： http://graphics.pixar.com/opensubdiv/docs/subdivision_surfaces.html
人们贪得无厌 只是为了确保已获得的美好生活不会失去怎么在淘宝买到听听水-认准徵１００６９０６８１３其他假冒
迷水购买地址-认准徵１００６９０６８１３其他假冒
听活水在线订购-认准徵１００６９０６８１３其他假冒
迷水付款商城-认准徵１００６９０６８１３其他假冒
迷水购买网-认准徵１００６９０６８１３其他假冒
迷水到付购买渠道-认准徵１００６９０６８１３其他假冒
广东迷幻商城-认准徵１００６９０６８１３其他假冒
听活水网址-认准徵１００６９０６８１３其他假冒
mj药水-认准徵１００６９０６８１３其他假冒
听活水20元-认准徵１００６９０６８１３其他假冒
g霸水购买网站-认准徵１００６９０６８１３其他假冒
在哪个网店买到听说水-认准徵１００６９０６８１３其他假冒
听水网店-认准徵１００６９０６８１３其他假冒
听水网店相关信息-认准徵１００６９０６８１３其他假冒
mj药网上商城-认准徵１００６９０６８１３其他假冒
迷水购买微信-认准徵１００６９０６８１３其他假冒
听水网店的货到付款是真的吗-认准徵１００６９０６８１３其他假冒
听水药水购买网站-认准徵１００６９０６８１３其他假冒
听活水在线订购-认准徵１００６９０６８１３其他假冒
迷水购买地址-认准徵１００６９０６８１３其他假冒
怎么在淘宝买到听听水-认准徵１００６９０６８１３其他假冒
迷水付款商城-认准徵１００６９０６８１３其他假冒
广东迷幻商城-认准徵１００６９０６８１３其他假冒
迷水购买网-认准徵１００６９０６８１３其他假冒
听活水网址-认准徵１００６９０６８１３其他假冒
迷水到付购买渠道-认准徵１００６９０６８１３其他假冒
听水药水购买网站-认准徵１００６９０６８１３其他假冒
求购听活水-认准徵１００６９０６８１３其他假冒
迷水购买地址-认准徵１００６９０６８１３其他假冒
怎么在淘宝买到听听水-认准徵１００６９０６８１３其他假冒
听活水网站-认准徵１００６９０６８１３其他假冒
离间水购买网址-认准徵１００６９０６８１３其他假冒
迷水付款商城-认准徵１００６９０６８１３其他假冒
听活水商城-认准徵１００６９０６８１３其他假冒
听水网店联系方式-认准徵１００６９０６８１３其他假冒
吐真水购买网站-认准徵１００６９０６８１３其他假冒
迷水商场-认准徵１００６９０６８１３其他假冒
喵喵快乐水购买渠道-认准徵１００６９０６８１３其他假冒
迷水购买-认准徵１００６９０６８１３其他假冒
听水网货到付款-认准徵１００６９０６８１３其他假冒
听水购买-认准徵１００６９０６８１３其他假冒
听活水39.8元套餐靠谱吗-认准徵１００６９０６８１３其他假冒
交大活水网站-认准徵１００６９０６８１３其他假冒
听活水使用方法-认准徵１００６９０６８１３其他假冒
活水网站-认准徵１００６９０６８１３其他假冒
乘乘水视频-认准徵１００６９０６８１３其他假冒
听活水使用后的真实感受-认准徵１００６９０６８１３其他假冒
听活水-认准徵１００６９０６８１３其他假冒
蓝精灵货到付款-认准徵１００６９０６８１３其他假冒
听水网官方入口-认准徵１００６９０６８１３其他假冒
听活水20元一桶-认准徵１００６９０６８１３其他假冒
乘乘水多少钱一瓶-认准徵１００６９０６８１３其他假冒
基督教活水网-认准徵１００６９０６８１３其他假冒
听水购买渠道-认准徵１００６９０６８１３其他假冒
交大活水-认准徵１００６９０６８１３其他假冒
听水药水购买网站-认准徵１００６９０６８１３其他假冒
求购听活水-认准徵１００６９０６８１３其他假冒
听水药水购买网站-认准徵１００６９０６８１３其他假冒
迷水购买地址-认准徵１００６９０６８１３其他假冒
怎么在淘宝买到听听水-认准徵１００６９０６８１３其他假冒
求购听活水-认准徵１００６９０６８１３其他假冒
听活水网址-认准徵１００６９０６８１３其他假冒
离间水购买网址-认准徵１００６９０６８１３其他假冒
迷水付款商城-认准徵１００６９０６８１３其他假冒
听水网店联系方式-认准徵１００６９０６８１３其他假冒
听活水商城-认准徵１００６９０６８１３其他假冒
听水购买-认准徵１００６９０６８１３其他假冒
听水网货到付款-认准徵１００６９０６８１３其他假冒
喵喵快乐水购买渠道-认准徵１００６９０６８１３其他假冒
听活水网站-认准徵１００６９０６８１３其他假冒
迷水购买-认准徵１００６９０６８１３其他假冒
听活水20元-认准徵１００６９０６８１３其他假冒
蓝精灵货到付款-认准徵１００６９０６８１３其他假冒
吐真水购买网站-认准徵１００６９０６８１３其他假冒
听活水-认准徵１００６９０６８１３其他假冒
交大活水网站-认准徵１００６９０６８１３其他假冒
听话饮料-认准徵１００６９０６８１３其他假冒
听水购买渠道-认准徵１００６９０６８１３其他假冒
活水网站-认准徵１００６９０６８１３其他假冒
听活水使用方法-认准徵１００６９０６８１３其他假冒
听水购买渠道官网-认准徵１００６９０６８１３其他假冒
交大活水-认准徵１００６９０６８１３其他假冒
迷水商场-认准徵１００６９０６８１３其他假冒
听水网店联系方式-认准徵１００６９０６８１３其他假冒
听水网官方入口-认准徵１００６９０６８１３其他假冒
催听迷货到付款官网-认准徵１００６９０６８１３其他假冒
听活水在线订购平台-认准徵１００６９０６８１３其他假冒
听水网安眠水购买-认准徵１００６９０６８１３其他假冒
崔迷水怎么买-认准徵１００６９０６８１３其他假冒
崔谜哪里买-认准徵１００６９０６８１３其他假冒
崔听迷商城-认准徵１００６９０６８１３其他假冒
台湾崔药商城-认准徵１００６９０６８１３其他假冒
乖乖听药商城软件-认准徵１００６９０６８１３其他假冒
迷商城-认准徵１００６９０６８１３其他假冒
乖乖听药商城旧版本-认准徵１００６９０６８１３其他假冒
迷水购买地址-认准徵１００６９０６８１３其他假冒
怎么在淘宝买到听听水-认准徵１００６９０６８１３其他假冒
乖乖听药商城支付方式-认准徵１００６９０６８１３其他假冒
崔药商城-认准徵１００６９０６８１３其他假冒
谜药商城-认准徵１００６９０６８１３其他假冒
绿箭口香糖迷幻系列-认准徵１００６９０６８１３其他假冒
迷幻口香糖网页版-认准徵１００６９０６８１３其他假冒
迷幻粉购买网站-认准徵１００６９０６８１３其他假冒
迷水购买地址-认准徵１００６９０６８１３其他假冒
迷幻谷商城官网-认准徵１００６９０６８１３其他假冒
进口迷幻粉-认准徵１００６９０６８１３其他假冒
美国进口迷幻粉官网-认准徵１００６９０６８１３其他假冒
迷幻粉购买网站-认准徵１００６９０６８１３其他假冒
迷水购买地址-认准徵１００６９０６８１３其他假冒
河北迷幻商城-认准徵１００６９０６８１３其他假冒
广州迷幻商城-认准徵１００６９０６８１３其他假冒
迷幻口香糖官网-认准徵１００６９０６８１３其他假冒
绿箭口香糖迷幻系列-认准徵１００６９０６８１３其他假冒
迷水付款商城-认准徵１００６９０６８１３其他假冒
迷幻之城-认准徵１００６９０６８１３其他假冒
广州迷幻商城体验-认准徵１００６９０６８１３其他假冒
迷幻商城官方网站-认准徵１００６９０６８１３其他假冒
迷幻粉购买网站-认准徵１００６９０６８１３其他假冒
弥漫商城-认准徵１００６９０６８１３其他假冒
迷商城-认准徵１００６９０６８１３其他假冒
迷幻商城是真的吗-认准徵１００６９０６８１３其他假冒
正品弥漫商城认准-徵１００６９０６８１３其他假冒
三轮子药商城认准-徵１００６９０６８１３其他假冒
三唑轮片购买网址认准-徵１００６９０６８１３其他假冒
弥漫商城认准-徵１００６９０６８１３其他假冒
三仑片购买渠道认准-徵１００６９０６８１３其他假冒
三唑轮片购买渠道-认准徵１００６９０６８１３其他假冒
三轮子是什么药-认准徵１００６９０６８１３其他假冒
三轮货到付款-认准徵１００６９０６８１３其他假冒
三座轮子购买渠道-认准徵１００６９０６８１３其他假冒
国产倒三轮-认准徵１００６９０６８１３其他假冒
三轮挫-认准徵１００６９０６８１３其他假冒
三轮子报价-认准徵１００６９０６８１３其他假冒
三轮子迷惑之王-认准徵１００６９０６８１３其他假冒
三坐轮子-认准徵１００６９０６８１３其他假冒
三轮子药商城-认准徵１００６９０６８１３其他假冒
三唑轮片购买网址-认准徵１００６９０６８１３其他假冒
三仑片购买渠道-认准徵１００６９０６８１３其他假冒
三唑轮片购买渠道-认准徵１００６９０６８１３其他假冒
三轮货到付款-认准徵１００６９０６８１３其他假冒
三座轮子购买渠道-认准徵１００６９０６８１３其他假冒
弥漫夜药水购买渠道-认准徵１００６９０６８１３其他假冒
迷幻商城新品 认准徵１００６９０６８１３其他假冒
迷幻商城网页版认准徵１００６９０６８１３其他假冒
婉情谷网上商城认准徵１００６９０６８１３其他假冒
迷幻谷商城app认准徵１００６９０６８１３其他假冒
幸福彼岸迷幻商认准徵１００６９０６８１３其他假冒城
广东迷幻商城官网认准徵１００６９０６８１３其他假冒
迷幻粉网购平台认准徵１００６９０６８１３其他假冒
谜药商城认准徵１００６９０６８１３其他假冒
迷幻谷商城 认准徵１００６９０６８１３其他假冒
婉情谷国际商城地址认准徵１００６９０６８１３其他假冒
迷幻商城app官方下载认准徵１００６９０６８１３其他假冒
爱神谷网药店商城认准徵１００６９０６８１３其他假冒
mj药水购买平台认准徵１００６９０６８１３其他假冒
迷商城购买网站 认准徵１００６９０６８１３其他假冒
迷幻商城体验 认准徵１００６９０６８１３其他假冒
迷幻商城官网 认准徵１００６９０６８１３其他假冒
幸福彼岸迷幻商城官网认准徵１００６９０６８１３其他假冒
迷幻商城 认准徵１００６９０６８１３其他假冒
迷幻谷商城官网入口认准徵１００６９０６８１３其他假冒
迷幻谷商城官网认准徵１００６９０６８１３其他假冒
婉情谷正品商城认准徵１００６９０６８１３其他假冒
24小时迷幻商城认准徵１００６９０６８１３其他假冒
广东迷幻商城 认准徵１００６９０６８１３其他假冒
迷幻商城最新版本认准徵１００６９０６８１３其他假冒
婉情谷商城认准徵１００６９０６８１３其他假冒
迷幻商城认准徵１００６９０６８１３其他假冒
迷幻商城迷幻粉购买平台认准徵１００６９０６８１３其他假冒
┌┍┎┏┐┑┒┓└┕┖┗┘┙┚┛├┝┞┟┠┡┢┣┤┥┦┧┨┩┪┫┬┭┮┯┰┱┲┳┴┵┶┷┸┹┺┻
┼┽┾┿╀╁╂╃╄╅╆╇╈╉╊╋─━│┃┄┅┆┇┈┉┊┋═║╒╓╔╕╖╗╘╙╚╛╜╝╞╟╠╡╢╣╤╥╦╧╨╩╪╫╬
┌┍┎┏┐┑┒┓└┕┖┗┘┙┚┛├┝┞┟┠┡┢┣┤┥┦┧┨┩┪┫┬┭┮┯┰┱┲┳┴┵┶┷┸┹┺┻
┼┽┾┿╀╁╂╃╄╅╆╇╈╉╊╋─━│┃┄┅┆┇┈┉┊┋═║╒╓╔╕╖╗╘╙╚╛╜╝╞╟╠╡╢╣╤╥╦╧╨╩╪╫╬
迷昏喷剂催《认准徵♥１００６９０６８１３》《其他假冒》
《认准徵♥１００６９０６８１３》《其他假冒》睡觉 药商城
崔药商城《认准徵♥１００６９０６８１３》《其他假冒》
《认准徵♥１００６９０６８１３》《其他假冒》婉情谷国际商城
爱神谷网药店商城《认准徵♥１００６９０６８１３》《其他假冒》
《认准徵♥１００６９０６８１３》《其他假冒》兴奋药网上医药商城药城网官网商城
帮助睡觉的药米施郎抗《认准徵♥１００６９０６８１３》《其他假冒》
《认准徵♥１００６９０６８１３》《其他假冒》眩晕药
红蜘蛛特效药商城《认准徵♥１００６９０６８１３》《其他假冒》
《认准徵♥１００６９０６８１３》《其他假冒》安眠药商城入口
mj药网上商城《认准徵♥１００６９０６８１３》《其他假冒》
┌┍┎┏┐┑┒┓└┕┖┗┘┙┚┛├┝┞┟┠┡┢┣┤┥┦┧┨┩┪┫┬┭┮┯┰┱┲┳┴┵┶┷┸┹┺┻
《认准徵♥１００６９０６８１３》《其他假冒》壹药网网上商城
男士专用药商城《认准徵♥１００６９０６８１３》《其他假冒》
《认准徵♥１００６９０６８１３》《其他假冒》无色无味强效睡眠药
崔药商城《认准徵♥１００６９０６８１３》《其他假冒》┌┍┎┏┐┑┒┓└┕┖┗┘┙┚┛├┝┞┟┠┡┢┣┤┥┦┧┨┩┪┫┬┭┮┯┰┱┲┳┴┵┶┷┸┹┺┻
《认准徵♥１００６９０６８１３》《其他假冒》安眠药商城
催听药商城《认准徵♥１００６９０６８１３》《其他假冒》
《认准徵♥１００６９０６８１３》《其他假冒》违禁药哪里能买到┌┍┎┏┐┑┒┓└┕┖┗┘┙┚┛├┝┞┟┠┡┢┣┤┥┦┧┨┩┪┫┬┭┮┯┰┱┲┳┴┵┶┷┸┹┺┻
晕药商城《认准徵♥１００６９０６８１３》《其他假冒》
《认准徵♥１００６９０６８１３》《其他假冒》强效睡眠货到付款
违禁药在哪里买《认准徵♥１００６９０６８１３》《其他假冒》
┌┍┎┏┐┑┒┓└┕┖┗┘┙┚┛├┝┞┟┠┡┢┣┤┥┦┧┨┩┪┫┬┭┮┯┰┱┲┳┴┵┶┷┸┹┺┻
┼┽┾┿╀╁╂╃╄╅╆╇╈╉╊╋─━│┃┄┅┆┇┈┉┊┋═║╒╓╔╕╖╗╘╙╚╛╜╝╞╟╠╡╢╣╤╥╦╧╨╩╪╫╬◢ ◣ ◥ ◤▁ ▂ ▃ ▄ ▅ ▆ ▇ █ ▉ ▊▋▌▍▎▏▓ ▔▕
┌┍┎┏┐┑┒┓└┕┖┗┘┙┚┛├┝┞┟┠┡┢┣┤┥┦┧┨┩┪┫┬┭┮┯┰┱┲┳┴┵┶┷┸┹┺┻
┼┽┾┿╀╁╂╃╄╅╆╇╈╉╊╋─━│┃┄┅┆┇┈┉┊┋═║╒╓╔╕╖╗╘╙╚╛╜╝╞╟╠╡╢╣╤╥╦╧╨╩╪╫╬
《认准徵♥１００６９０６８１３》《其他假冒》男士专用药商城
网上药店商城官网《认准徵♥１００６９０６８１３》《其他假冒》┌┍┎┏┐┑┒┓└┕┖┗┘┙┚┛├┝┞┟┠┡┢┣┤┥┦┧┨┩┪┫┬┭┮┯┰┱┲┳┴┵┶┷┸┹┺┻
《认准徵♥１００６９０６８１３》《其他假冒》买药网站迷幻商城
谜药商城《认准徵♥１００６９０６８１３》《其他假冒》
《认准徵♥１００６９０６８１３》《其他假冒》崔药商城
mj药网上商城视频效果《认准徵♥１００６９０６８１３》《其他假冒》
《认准徵♥１００６９０６８１３》《其他假冒》广州迷幻商城官网
正品弥漫商城《认准徵♥１００６９０６８１３》《其他假冒》┌┍┎┏┐┑┒┓└┕┖┗┘┙┚┛├┝┞┟┠┡┢┣┤┥┦┧┨┩┪┫┬┭┮┯┰┱┲┳┴┵┶┷┸┹┺┻┌┍┎┏┐┑┒┓└┕┖┗┘┙┚┛├┝┞┟┠┡┢┣┤┥┦┧┨┩┪┫┬┭┮┯┰┱┲┳┴┵┶┷┸┹┺┻
《认准徵♥１００６９０６８１３》《其他假冒》23迷幻商城
购买药品的网站《认准徵♥１００６９０６８１３》《其他假冒》
《认准徵♥１００６９０６８１３》《其他假冒》违禁药哪里能买到
安眠药在线购买网站《认准徵♥１００６９０６８１３》《其他假冒》
《认准徵♥１００６９０６８１３》《其他假冒》安眠药购买平台
安眠药商城入口《认准徵♥１００６９０６８１３》《其他假冒》┌┍┎┏┐┑┒┓└┕┖┗┘┙┚┛├┝┞┟┠┡┢┣┤┥┦┧┨┩┪┫┬┭┮┯┰┱┲┳┴┵┶┷┸┹┺┻
《认准徵♥１００６９０６８１３》《其他假冒》安眠药网上购买
乖乖听药商城购物方式《认准徵♥１００６９０６８１３》《其他假冒》┌┍┎┏┐┑┒┓└┕┖┗┘┙┚┛├┝┞┟┠┡┢┣┤┥┦┧┨┩┪┫┬┭┮┯┰┱┲┳┴┵┶┷┸┹┺┻
三轮子药商城三轮子药效果《认准徵♥１００６９０６８１３》《其他假冒》
三轮片购买渠道《认准徵♥１００６９０６８１３》《其他假冒》
三座轮子药《认准徵♥１００６９０６８１３》《其他假冒》
三轮子药三坐轮正品《认准徵♥１００６９０６８１３》《其他假冒》
相关推荐
┌┍┎┏┐┑┒┓└┕┖┗┘┙┚┛├┝┞┟┠┡┢┣┤┥┦┧┨┩┪┫┬┭┮┯┰┱┲┳┴┵┶┷┸┹┺┻
┼┽┾┿╀╁╂╃╄╅╆╇╈╉╊╋─━│┃┄┅┆┇┈┉┊┋═║╒╓╔╕╖╗╘╙╚╛╜╝╞╟╠╡╢╣╤╥╦╧╨╩╪╫╬◢ ◣ ◥ ◤▁ ▂ ▃ ▄ ▅ ▆ ▇ █ ▉ ▊▋▌▍▎▏▓ ▔▕
┌┍┎┏┐┑┒┓└┕┖┗┘┙┚┛├┝┞┟┠┡┢┣┤┥┦┧┨┩┪┫┬┭┮┯┰┱┲┳┴┵┶┷┸┹┺┻
┼┽┾┿╀╁╂╃╄╅╆╇╈╉╊╋─━│┃┄┅┆┇┈┉┊┋═║╒╓╔╕╖╗╘╙╚╛╜╝╞╟╠╡╢╣╤╥╦╧╨╩╪╫╬
三唑轮片购买方式《认准徵♥１００６９０６８１３》《其他假冒》
三唑轮片购买网站《认准徵♥１００６９０６８１３》《其他假冒》
三唑轮片合法购买渠道《认准徵♥１００６９０６８１３》《其他假冒》
《认准徵♥１００６９０６８１３》《其他假冒》三唑迷片
《认准徵♥１００６９０６８１３》《其他假冒》三仑片购买
《认准徵♥１００６９０６８１３》《其他假冒》三唑轮片购买网站
《认准徵♥１００６９０６８１３》《其他假冒》三唑轮片购买方式
《认准徵♥１００６９０６８１３》《其他假冒》三唑轮片合法购买渠道
《认准徵♥１００６９０６８１３》《其他假冒》三唑咪仑药店
相关搜索
┌┍┎┏┐┑┒┓└┕┖┗┘┙┚┛├┝┞┟┠┡┢┣┤┥┦┧┨┩┪┫┬┭┮┯┰┱┲┳┴┵┶┷┸┹┺┻
┼┽┾┿╀╁╂╃╄╅╆╇╈╉╊╋─━│┃┄┅┆┇┈┉┊┋═║╒╓╔╕╖╗╘╙╚╛╜╝╞╟╠╡╢╣╤╥╦╧╨╩╪╫╬◢ ◣ ◥ ◤▁ ▂ ▃ ▄ ▅ ▆ ▇ █ ▉ ▊▋▌▍▎▏▓ ▔▕
┌┍┎┏┐┑┒┓└┕┖┗┘┙┚┛├┝┞┟┠┡┢┣┤┥┦┧┨┩┪┫┬┭┮┯┰┱┲┳┴┵┶┷┸┹┺┻
┼┽┾┿╀╁╂╃╄╅╆╇╈╉╊╋─━│┃┄┅┆┇┈┉┊┋═║╒╓╔╕╖╗╘╙╚╛╜╝╞╟╠╡╢╣╤╥╦╧╨╩╪╫╬
《认准徵♥１００６９０６８１３》《其他假冒》三仑片购买
《认准徵♥１００６９０６８１３》《其他假冒》三唑轮片购买网站
《认准徵♥１００６９０６８１３》《其他假冒》三唑轮片购买方式
《认准徵♥１００６９０６８１３》《其他假冒》三唑轮片合法购买渠道
《认准徵♥１００６９０６８１３》《其他假冒》三唑咪仑药店
《认准徵♥１００６９０６８１３》《其他假冒》三唑迷片
《认准徵♥１００６９０６８１３》《其他假冒》三唑轮片哪里有卖
《认准徵♥１００６９０６８１３》《其他假冒》三唑轮片
《认准徵♥１００６９０６８１３》《其他假冒》三唑咪仑会睡死吗
太高级了，看不懂
太高级了，看不懂
太高级了，看不懂