本文介绍的技术，适用于硬表面平滑细分建模，且包含了特定于 Catmull-Clark 细分方案的技术，所以有些部分要能灵活变通。
拓扑
构造良好的细分网格，应该具有以下几个重要的特性：
·它主要由规则的面组成(四边面、三边面)；
·可包含一些特殊的顶点；
·可以有效的描述了预期的形状；
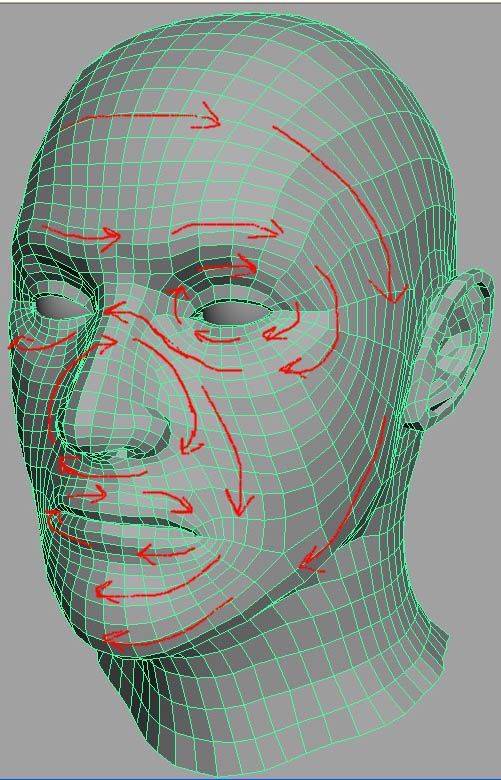
·它是基于拓扑流结构的；
使用较少的分段
虽然多边形建模中，需要大量的分段来近似平滑曲面，但细分模型需要的控制顶点明显更少。
大多数情况下，6 个分段足以创建精确的圆形，而背景对象通常 4 个分段就够了。
避免高边顶点
高边顶点是指由 4 个以上相邻边连接的顶点，在添加平滑细分时，会导致以下几个问题：
·当旋转形状的顶点被三角形环绕时，Catmull-Clark 细分方案，会生成波形曲面，如下图。
·对性能会产生非常大的影响。
·目前，对于高边顶点的最大边值，OpenSubdiv 有一个由 GPU 着色器产生的硬性约束(在当前的硬件上约为 27)
相反，你可以用一些拓扑策略来封顶旋转形状：
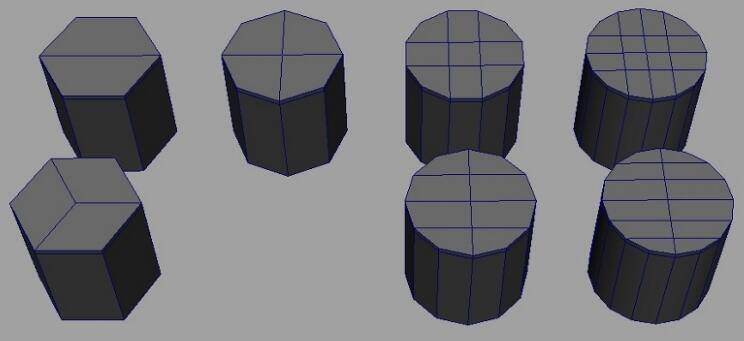
注意，所有这些圆柱体只使用了四边形面，并且除了左下角的示例，所有封顶中的顶点边数都是 4。
循环边转换
通常我们需要改变网格表面上的顶点密度：比如手指周围的区域，比相对简单的手掌区域，需要更多的控制顶点，所以有效的处理这些循环边拓扑结构的转换是很重要的，其中一个策略是使用特殊的顶点，例如本例中，是一个 5 边顶点，将 3 个循环边扩展为 5 个。
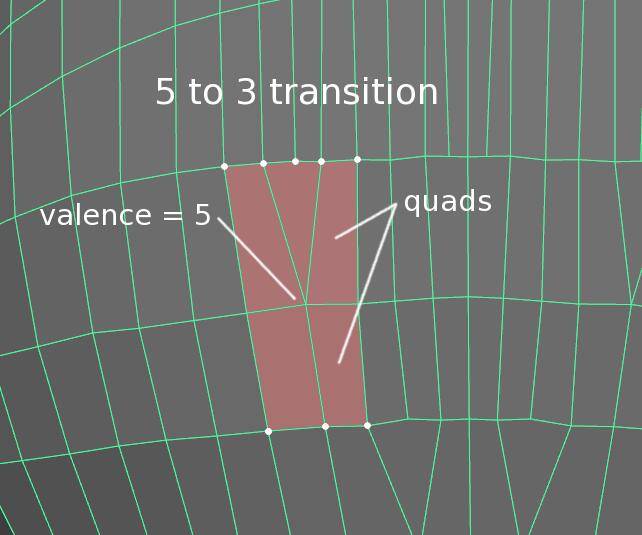
实用拓扑入门
一个真实的例子，展示了具有较少的拓扑结构，很少的特殊顶点，没有高边极点，并能生成细节满满的形状。
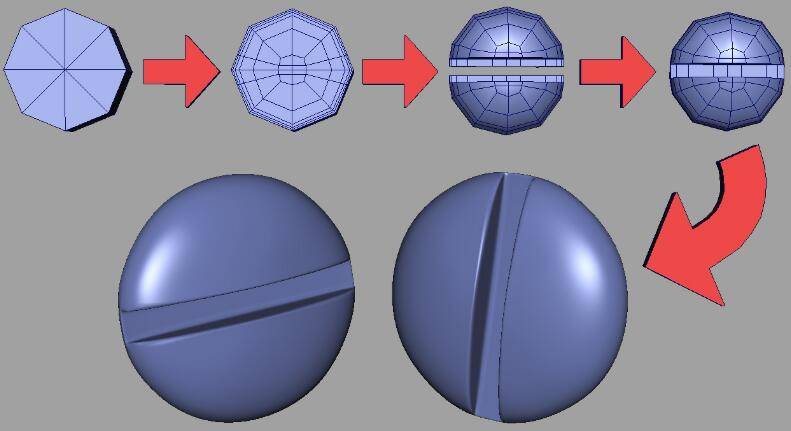
三角形与 N-Gons
少量的使用非四边面可以非常有效的聚集 3 个或更多的循环边(N-Gons)，这些问题通常发生在高变形区域或曲率脊点(例如、手臂与驱赶的连接)。在这些关键的区域战略性的放置一个五边形，可以确保表面保持光滑，同时也可以产生复杂的拓扑流结构。
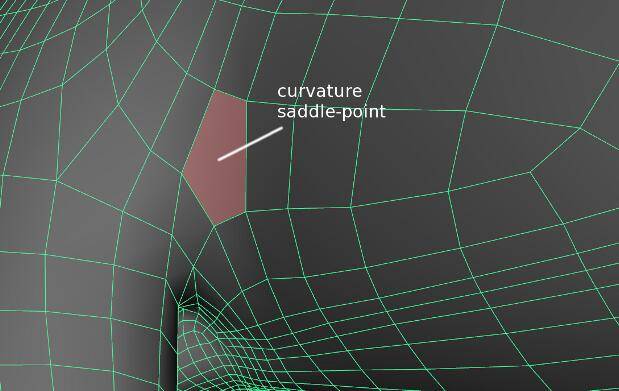
半锐折痕
它是一个非常强大的工具，可以对边和顶点进行锐度值标记。其范围为 0(平滑)~10(锐利)，如果可以的话，使用半锐折痕来替代循环边，通常会更方便，但可能增加额外计算开销。
相关推荐
【R站洪瑞&穆他】好评如潮！《C4D电商产品建模实战宝典》硬表面细分曲面建模教程(72集/20小时+)精讲班 第一季 ~ 中文视频教程 超值特惠中...
【R站洪瑞&穆他】2019钜惠《C4D电商产品建模终极宝典》硬表面细分曲面建模教程 (100集+/28小时+) 精讲班 第二季~ Hardsurface Modeling 中文视频教程 超值预售中…
海棠大厅微信6人拼三张房卡【—QQ—89223577】无需要打开直接添加▊1新道游系列▊大圣系列▊新神兽系列▊老神兽系列▊悠悠系列H5等游戏房卡----光明大厅十九人牛牛房卡【—QQ—89223577】无需要打开直接添加▊1新道游系列▊大圣系列▊新神兽系列▊老神兽系列▊悠悠系列H5等游戏房卡大厅